本記事は CyberAgent AI Lab Advent Calendar 2025 第1日目の記事です。

はじめに

メリークリスマス！🎄🎅

サイバーエージェント AI Lab Market & Behavioral Design（MBD）チームのみーとみ（@miiitomi）です。 ちなみに9月まで経済学社会実装（EconSI）チームという名前でしたが10月からチーム名が変更になりました。AI Lab MBDチームをよろしくお願いします🙇

ところで皆さん、日常生活の中でこんな状況ありませんか！？（唐突）

あるサッカーチームが、選手のグッズをランダムにファンに配りました。ファンはそれぞれグッズを受け取りましたが、ファンにはそれぞれ推し選手がおり、推し選手のグッズが得られている人もいれば、推し選手でない選手のグッズを受け取ったファンもいます。今日あるファンの呼びかけで、グッズを手にしたファン達が集まってグッズを交換することにしました。参加者が誰も損することなく皆が納得するようにグッズ交換するためにはどのようにしたら良いでしょうか？

推し活のグッズ交換、クリスマスパーティのプレゼント交換など、参加者が1人1つ提供できるものを持っていて、それらを各々の希望に応じて交換したい、という状況はたまにあるかと思います。 そのような状況で適切な交換方法を求める TTC（Top Torading Cycle）アルゴリズム という古典的なアルゴリズムが古くから知られています（Shapley and Scarf (1974)¹）。

今回はそのTTCアルゴリズムを簡単に実行できるWEBアプリケーション「最適交換アプリ」を作成してみました。以下ではそのTTCアルゴリズムを簡単に紹介しますので、ぜひアプリの方を試しながらお読みください。

問題設定

考えたいのは、以下のような状況です。

• 参加者が $N$ 人おり、それぞれ $1$ さん、$2$ さん、…、$N$ さんと呼ぶ。
• 参加者はそれぞれ、提供できるものを1つずつ（$w_1$、$w_2$、…、$w_N$）用意している。
• 参加者はそれぞれ、用意されたもの $N$ 個に対して希望順位を持っている。

例えば、$5$ 人の場合では以下のような例が考えられます。

例1

• 参加者は $1$ さん、$2$ さん、$3$ さん、$4$ さん、$5$ さんの $5$ 人。それぞれ $w_1, w_2, w_3, w_4, w_5$ を用意してきた。
• それぞれの希望は以下の通り。

  	$1$ さん	$2$ さん	$3$ さん	$4$ さん	$5$ さん
  第 $1$ 希望	$w_3$	$w_4$	$w_4$	$w_5$	$w_3$
  第 $2$ 希望	$w_2$	$w_1$	$w_5$	$w_1$	$w_5$
  第 $3$ 希望	$w_1$	$w_2$	$w_3$	$w_3$	$w_1$
  第 $4$ 希望	$w_4$	$w_5$	$w_1$	$w_2$	$w_2$
  第 $5$ 希望	$w_5$	$w_3$	$w_2$	$w_4$	$w_4$

これに対して、私たちが欲しいのは以下のようなものです。

• $N$ 人がそれぞれ欲しいものの希望順位を提出したときに、その希望から誰も損せず皆が納得する交換の仕方を自動で計算してくれるもの。

参加者が2-3人であれば話あって適切に交換することができるかもしれませんが、人数が多くなってくると皆が納得する交換の仕方を決めるのは容易ではないでしょう。 それを自動で決めてくれるものが今回私たちが欲しいものです。

皆が納得するために必要な条件

「誰も損せず皆が納得する交換の仕方」を見つけたいと述べましたが、それは具体的にはどのようなものでしょうか？ 上述の例をもとに考えていきたいと思います。

条件1.　誰も損しない（個人合理性）

例1において、数字の小さい順に $1$ さんから好きなものを取っていく方法で交換の仕方を決めたとしましょう。すると次のようになります。

それぞれが持っていくもの

• $1$ さん：$w_3$（第 $1$ 希望）
• $2$ さん：$w_4$（第 $1$ 希望）
• $3$ さん：$w_5$（第 $2$ 希望）
• $4$ さん：$w_1$（第 $2$ 希望）
• $5$ さん：$w_2$（第 $4$ 希望）

この方法では順番が最後になる $5$ さんが著しく不利であり、さらに $5$ さんは自分が持ってきたものよりも希望度の低い $w_2$ を持ち帰ることになっています。 このような状況では $5$ さんは交換に参加することでむしろ損をしており、このような交換の仕方は $5$ さんにとって納得できるものではないでしょう。

したがって、交換の仕方が満たすべき条件の1つ目は次のようなものになります。

条件1.　個人合理性

参加者は皆、自身が持ってきたものか、またはそれ以上に希望するものを得る。

条件2.　全員が同意できるようなそれ以上の改善はない（パレート効率性）

例1において、$1$ さんと $2$ さんは話していて、二人が持ってきたものを交換することで二人とも得することに気が付きました。また、$3$ さんと $4$ さんも、二人のものを交換することに同意しました。 よって $1$ さんと $2$ さん、$3$ さんと $4$ さんが交換すると、結果は以下のようになります。

• $1$ さん：$w_2$（第 $2$ 希望）
• $2$ さん：$w_1$（第 $2$ 希望）
• $3$ さん：$w_4$（第 $1$ 希望）
• $4$ さん：$w_3$（第 $3$ 希望）
• $5$ さん：$w_5$（第 $2$ 希望）

ですが、この交換の仕方ではまだベストではないようです。$4$ さんが今持っている $w_3$と、$5$ さんの $w_5$ を交換すると、さらにまた二人とも得することができます。

このような、誰も損することなく誰かが得できるような、全員が同意できる改善が存在するうちは、最適な交換とは言えないでしょう。よって、2つ目の条件は以下のようなものになります。

条件2.　パレート効率性

誰も損することなく誰かが得できるような、全員が同意できる今以上の改善はない。

条件3.　嘘をつくことで得をすることがなく、皆が希望を正直に申告することが常に最適である（耐戦略性）

条件3は例を用いて説明するには複雑になるので簡単に説明します。

私たちが欲しいものは「$N$ 人がそれぞれ欲しいものの希望順位を提出したときに、その希望から誰も損せず皆が納得する交換の仕方を自動で計算してくれるもの」と説明しました。 交換の主催者はもちろん参加者全員の希望を詳細に知っているとは限らず、参加者に希望を申告してもらう必要があります。

ここで、「本当は $w_3$ が一番欲しいけど、人気そうだから $w_5$ を第一希望ってことにしとこう」などのように、本当の希望を申告しない人がいたらどうでしょうか？ 嘘の申告をすることで得することがありうるようなルールになっていると、交換結果が嘘の申告に基づくもののため本当の希望のもとで適切であるかどうかが分からないだけでなく、参加者は自分が得するためにはどのように申告するべきか戦略を考える負担がかかり、正直者が損をするような状況になっている場合もあり得ます。 そのような状況はあまり望ましいものではなく、できれば参加者にとって本当の希望を正直に申告することが常に一番得であるようなルールであることが、参加者にとっても主催者にとっても望ましいでしょう。

したがって、望ましいルールの条件の3つ目は以下のようなものになります。

条件3.　耐戦略性

参加者にとって本当の希望を正直に申告することが常に一番得であるようなルールである。

TTCアルゴリズム

いよいよ適切な交換の仕方を求める「TTCアルゴリズム」の説明にうつります。TTCアルゴリズムとは以下のようなものです。

TTC（Top Trading Cycle）アルゴリズム

1. $N$ 人の参加者それぞれに対応する点を持つ、有向グラフを作る。始め辺は張られていない。
2. 有向グラフに点が存在する限り、以下を繰り返す。
   • いま残っている参加者 $i$ それぞれについて、以下を行う。
     • $i$ から辺が張られていない場合、いま残っている参加者が用意してきたもののうち $i$ にとって最も希望度の高いものを $w_j$ とし、点 $i$ から点 $j$ に向けて有向辺を張る（$j = i$ の場合も起こり得る）。
   • 有向グラフから閉路を見つけ、それを $i_1 \to i_2 \to … \to i_K \to i_1$ とする。
   • 参加者 $i_1$ は $w_{i_2}$ を、参加者 $i_2$ は $w_{i_3}$ を、… 参加者 $i_K$ は $w_{i_1}$ を得るものとし、その閉路に含まれる点とその点が含まれる辺を全てグラフから取り除く。

例1に対してこのTTCアルゴリズムを適用すると、結果は次のようになります。

• 点 $1$ から 点 $3$、点 $2$ から 点 $4$、点 $3$ から点 $4$、点 $4$ から点 $5$、点 $5$ から点 $3$ に有向辺が張られる。
• $3 \to 4 \to 5 \to 3$ の閉路ができたため、参加者 $3$ が $w_4$ を、参加者 $4$ が $w_5$ を、参加者 $5$ が $w_3$ を得て、グラフから取り除かれる。
• 点 $1$ から 点 $2$、点 $2$ から点 $1$ に有向辺が張られる。
• $1 \to 2 \to 1$ の閉路ができたため、参加者 $1$ が $w_2$ を、参加者 $2$ が $w_1$ を得て、グラフから取り除かれる。
• グラフが空になっため終了し、結果は以下となる。
  • $1$ さん：$w_2$（第 $2$ 希望）
  • $2$ さん：$w_1$（第 $2$ 希望）
  • $3$ さん：$w_4$（第 $1$ 希望）
  • $4$ さん：$w_5$（第 $1$ 希望）
  • $5$ さん：$w_3$（第 $1$ 希望）

この結果は、条件1（個人合理性）と、条件2（パレート効率性）を満たしています。

証明は省略しますが、この例に限らず、TTCアルゴリズムは条件1と条件2を満たす全員が納得する交換の仕方を結果として返します。 またTTCアルゴリズムを用いて交換するルールは、条件3の耐戦略性を満たす、つまり参加者は皆自身の本当の希望を正直に申告することが常に参加者にとって最適であることが知られています。

最適交換アプリ

はじめにでも述べたとおり、このTTCアルゴリズムを簡単に実行できる最適交換アプリを作成しました。 ぜひ参加者同士で用意したものを交換したい状況でお使いください！

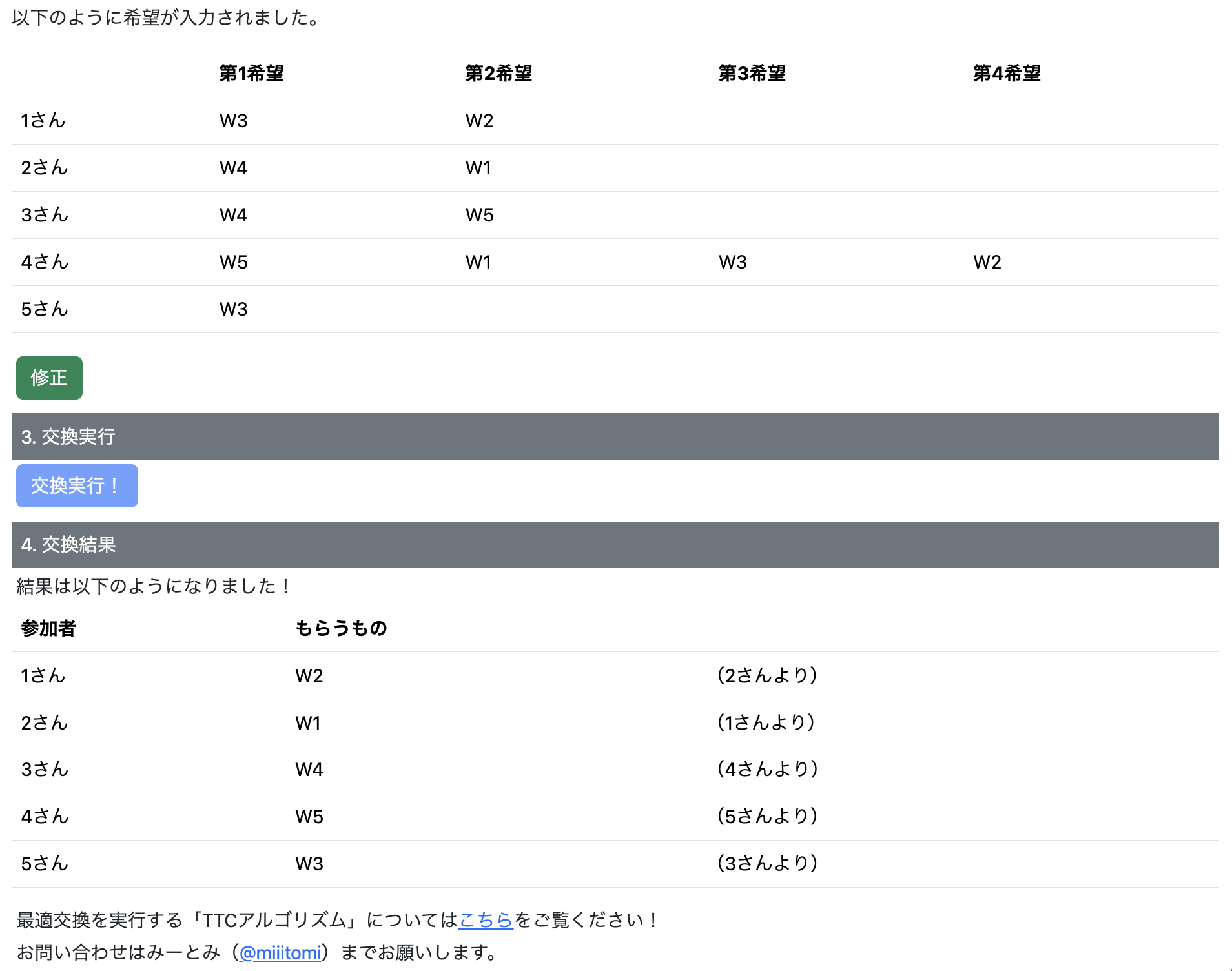
上の例1を実行してみると以下のようになります（ちなみにTTCアルゴリズムでは自分自身の用意してきたもの以下の希望順位は必要ないため、アプリでは自分自身のものより希望するもののみを入力させるようにしています）。

おわりに

今回のように、人や人・人やものを人々の希望に応じて適切にマッチさせる方法を考える分野として「マッチング理論」という分野があり、マッチング理論などの知見を現実の市場・制度の設計に活用しようという分野として「マーケットデザイン」という分野があります。 私たちAI Lab Market & Behavioral Designチームでは、このマッチング理論・マーケットデザインの分野において研究して論文を発表するとともに、保育所利用調整における保育所と児童のマッチングなど、実際のマッチング制度の設計・開発も行っています。 ちなみに私たちのチームの保育所利用調整マッチングにおける取り組みは、この度書籍 「［AIと経済学］で もっとよくなる保育政策」としてまとめましたので、ご興味のある方はよかったらご覧ください。

また、マッチング理論における他のアルゴリズムである、2グループ間の人を希望に応じて適切にマッチさせるDAアルゴリズムは こちら、希望に応じてものを公平に配るための最適なくじ引きを作るPSアルゴリズムは こちら で実行できるアプリを用意していますので、そちらも合わせてお試しいただけると嬉しいです。

明日のCyberAgent AI Lab Advent Calendar 2025は同じチームの竹浪さんから、同じくマッチングネタで「よいマッチングのために、あえて「マッチング」しないアプローチ」についての記事とのことです！ お楽しみに〜〜🎄